Steinbruch-Druseltal.de

retrosignaling

- mit Standard-QM

steinbruch-druseltal.de/retrosignalingStQM.pdf
Ergänzung 17.7.:
Die roten Kurven sind doch Regressionskurven, keine Erwartungskurven. (Regressionskurven mit Einschränkungen).
Die Erwartungskurve (Wahrscheinlichkeitsverteilung) für “alle Nebenphotonen auf D1” lautet f1(x)=(sin(1917.34x)cos(4473.8x)/(1917.34x))²

- mit “super”-QM (Peoch79)

steinbruch-druseltal.de/DraftArticlesOnRetrocausality.pdf

28.8. Fortsetzung Retrosignaling mit Standard-Quantenphysik

Korrektur: Die roten Kurven bei Kim...Scully sind doch Interpolationskurven.
Ich dachte es sind keine Interpolationskurven, weil zu ungenau, sondern Wahrscheinlichkeitskurven (R01-4 mit noch einem geometrischen Umstand).

fi(x):=R0i Wahrscheinlichkeitskurven,
R0iint rote Interpolationskurven, i=1,..,4

         R01int+R02int       Messwerte für R01
                                       + Messwerte für R02

w=702.2nm
a=0.3mm
d=0.7mm
b=?

Brennweite Linse nicht angegeben, Winkel muss klein sein (“far field condition“),
Schätzung b=0,7m , damit stimmen die Kurven mit den mm-Angaben auf x-Achse überein:

f1(x)=(sin(1917.34x)cos(4473.8x)/(1917.34x))²  |Wahrscheinlichkeit für x-Koordinate wenn
f2(x)=(sin(1917.34x)sin(4473.8x)/(1917.34x))²  |BSon und alle Nebenphotonen auf D1 bzw. D2

f1(x)+f2(x)=(sin(1917.34x)/(1917.34x))² = f3(x)+f4(x)
Wahrscheinlichkeit wenn alle Photonen auf einen Schirm (BSon und BSoff nicht unterscheidbar)

Korrigierte Bilder Wahrscheinlichkeitskurven und Funktionsdiagramm:

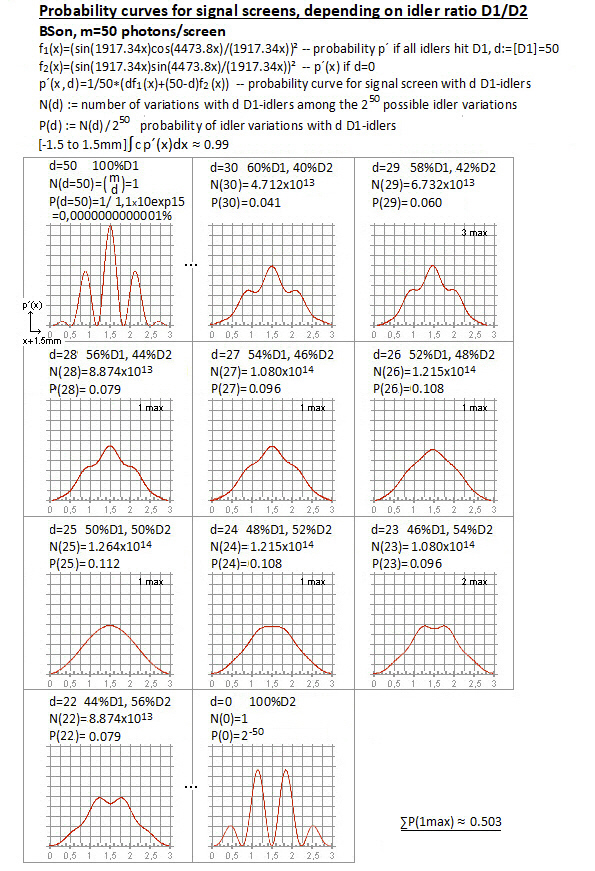
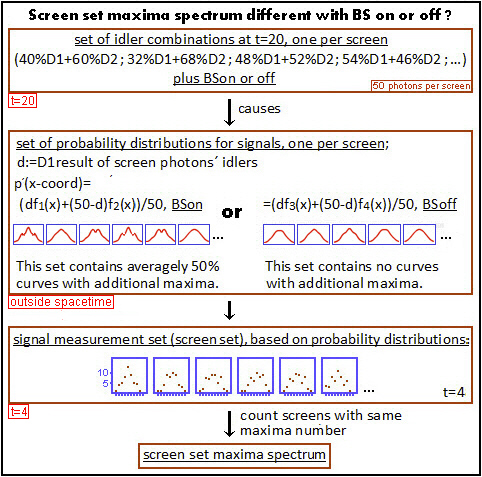
Somit haben 50% der Bildschirm-Wahrscheinlichkeitskurven mehr als 1 Maximum, statt nur 4% wie bei der Rechnung mit den falschen Kurven. Das bedeutet erheblich weniger Rauschen.

Die weiteren Rauschquellen:

RQ1) Viele Photonen landen im Blech um den Doppelspalt.
Zeichnung Blech, Doppelspalt, Lichtkegel:

gelb: ca. 99%-Lichtkegel.
Wenn hier der Durchgang ungefähr der Fläche entspricht, bleiben ca.65% der Photonen im Blech hängen. Die Blechphotonen können registriert und innerhalb weniger ns ersetzt werden.
Man schickt also ungefähr 120 Photonen los (damit nicht zu viele durchgehen), dann zwei weitere Wellen, dann kommen ungefähr 50 durch. Je nachdem wie viele im Versuchsverlauf verloren gehen, muss man daher eine exakte Analyse für “ungefähr 50“ Photonen durchführen und beweisen, dass dieses Rauschen nicht zu stark ist.

RQ2) Schichtdicke des Verschränkungskristalls hinter dem Doppelspalt.
Dadurch könnte eine geringe Ortsungenauigkeit enstehen, und zusätzlich könnte ein (kleiner) Prozentsatz hängenbleiben.

RQ3) In Linsen und Spiegeln können einige wenige Photonen hängenbleiben/einschlagen.

RQ4) Messstellen sind auch nicht ganz 100% exakt.

Gegen Rauschen helfen evtl technische Weiterentwicklungen, auch mit energiereicheren Photonen.
Hängengebliebene Photonen können evtl detektiert und ersetzt werden.
Ich versuche technische Details zu ermitteln um eine Beweisführung mit Rauschen durchzuführen.

Fehlende Funktionen f3 , f4

f3(x)+f4(x) = (sin(1917.34x)/(1917.34x))² aber weitere explizite Info über f3 und f4 fehlt im Text.
Der Graph R03int sieht aus wie hingeschissen:
Die Messbereiche sind anders als bei R01/2, obwohl im Text ausdrücklich darauf hingewiesen wird, dass alle Messkurven in einem Durchgang aufgestellt werden müssen, und ca. 20% der Photonen fehlen. Vielleicht war der Strahlteiler schief oder die Messgeräte schlecht.
Dies stört nicht bei der Aufgabenstellung, es sollte nur nachgewiesen werden, dass keine Interferenz auftritt. Aber es stört bei der statistischen Analyse von parallelen Versuchen ohne Coincidence counter, vielleicht Absicht.

http://volkscomputer.biz/RetrosignalingwithStandardQMJan21.pdf